Escaping a Jupyter Maze

My last article was a bit of a diatribe on why programming can be tough. As a practical example, I walked through some of the challenges I ran into while writing a simple maze generator. Programming hell aside, I did have fun creating mazes. So much fun, that I decided to write a follow up program that attempts to traverse the generated mazes.

This article documents how I went about creating a simple AI that explores a maze.

Autonomous Agents#

I’m slowly working my way up to creating a robust simulation type game. To get there, I’ve been exploring different procedural generation and AI techniques. From an AI perspective I’m interested in the concept of an intelligent agent.

An agent is a self contained entity in the software that decides for itself how to accomplish a set of tasks based on what it can observe about its environment. More formally, an agent is:

An agent is anything that can be viewed as perceiving its environment through sensors and acting upon that environment through actuators.

For my purposes, an agent only needs to focus on how to move around the maze and attempt to escape. That said, this is an opportunity to think through how to create agents for a wider set of use cases. With that in mind, I want an agent that:

• Can be easily expanded. For example, I’d like to try multiple traversal algorithms.
• Behaves like a living creature. Even though my little program represents agents as just a box, I want them to at a fundamental level act like they’re alive.
• Be water tight. I don’t want the agent’s abstraction to leak into the rest of the code base. Conversely, I want to prevent the agents from knowing too much about the other systems in the program.

A Humble Agent#

With the requirements listed above in hand, I’ve formed the model of thinking about agents as:

• What is the agent’s state?
• What does the agent look like?
• What is the agent’s behavior?

With the maze use case, an agent’s state is defined as the combination of: location, last location, and orientation.

An agent’s appearance is simply a colored square. To prevent agents from knowing about the graphics library, rendering is handled elsewhere. I want agents to be distinguished individually. To do that each agent can have a crest. Currently, a crest is just a color.

Behold My Humble Agent

class Agent:
  _location: Point # The maze coordinate of where the agent currently is.
  _last_location: Point # The last place the agent remembers it was.
  _facing: Direction # The direction the agent is facing.
  _crest: str # The color to represent the agent.

  def __init__(self, crest='blue') -> None:
    """Create a new instance of an agent."""
    self._crest = crest
    self._location = Point(0,0)
    self._last_location = Point(0,0)

  # Object Properties excluded for brevity

  def face(self, direction: Direction) -> None:
    """Set the direction the agent is facing."""
    self._facing = direction

  def move_to(self, new_location: Point):
    """Tell the agent to walk to the new location in the maze."""
    self._last_location = self.location
    self._location = new_location

  def maze_strategy(self, strategy: Callable[..., None]) -> None:
    """Assign a maze traversal algorithm to the agent."""
    self._maze_strategy = strategy

  def explore(self, maze: Maze) -> None:
    """Perform one step of the assigned maze traversal strategy."""
    self._maze_strategy(self, maze)

Agents are composable. To get a new type of agent we assign different capabilities. In the below example we can create an explorer by assigning it its own unique algorithm for how it traverses the maze.

brave_explorer = Agent('green')
brave_explorer.maze_strategy(explorer_algorithm)
brave_explorer.move_to(Point(14,22)) # Set the initial location.
brave_explorer.face(Direction.SOUTH)

# In the simulation's main loop, the agent performs one action per frame
# and is then rendered.
for frame in range(num_frames):
  brave_explorer.explore(maze)
  draw_agent(brave_explorer)

Maze Traversal Strategies#

On to the business of escaping a maze. In my little program a new maze is randomly generated on each program run. Agents always start from the center. They can escape by leaving from the maze’s entrance (always on the north boundary) or the exit (always on the south boundary).

The Clueless Walker#

A general rule of thumb in programing is to always try the simplest thing first. In this case, the simplest approach to traversing a maze is to just have the agent walk in a straight line until it encounters a wall. When that happens, the agent tries to go right. If it can’t, it tries to go left. If it can do neither, then it turns around and goes back the way it came.

def random_walk(agent: Agent, maze: Maze):
  """
  Given an agent, have them randomly choose a room to go to next, then move.
  """
  # 1. Get the current room the agent is in.
  current_room = maze.cell(agent.location)

  #  If the agent is at the entrance or exit of the maze, then stop.
  if current_room is maze.starting_cell or current_room is maze.exit_cell:
    return;

  # 2. Find all the walls that have doors in that room.
  possible_directions: List[Direction] = current_room.open_sides()

  # 3. Find the next direction to go.
  next_direction = find_next_direction(agent, possible_directions)

  # 4. Find the location of the room the open door connects to.
  next_location: Point = maze.find_adjacent_neighbor(next_direction, agent.location)

  # 5. Move the agent to the next room.
  agent.face(next_direction)
  agent.move_to(next_location)

The code above is straight forward. The only interesting bit is the find_next_direction function, which is listed below. It leverages the concept of direction and orientation. Both of which are implemented as enumerations.

def find_next_direction(agent: Agent, possible_directions: list[Direction]) -> Direction:
  """The agent is facing a direction. I think it should continue in the same direction
  if possible. If not, it should try right, then left. Finally, backtrack."""
  current_orientation: dict[Orientation, Direction] = DIR_ORIENTATION[agent.facing]
  if agent.facing in possible_directions:
    next_direction = agent.facing
  elif current_orientation[Orientation.RIGHT] in possible_directions:
    # Is there a door to the right?
    next_direction = current_orientation[Orientation.RIGHT]
  elif current_orientation[Orientation.LEFT] in possible_directions:
    # Is there a door to the left?
    next_direction = current_orientation[Orientation.LEFT]
  elif current_orientation[Orientation.BEHIND] in possible_directions:
    # Go back the way we came?
    next_direction = current_orientation[Orientation.BEHIND]
  else:
    raise Exception("We\'re walled in! No possible doors found.")
  return next_direction

The random walker agent is pretty hopeless. You can see in the GIF below that the agent is unlikely to escape the maze and become stuck very quickly.

Wall Follower Algorithm#

So randomly walking, isn’t going to solve the problem. The next simplest thing I can think of to improve the agent’s chances of making it out of the maze alive is to leverage a classic maze traversal strategy. Fortunately, there are several to choose from.

For my money, I think the Wall Follower Algorithm is the simplest technique. It is:

The agent places a "hand" on a wall (left or right) and walks forward,
never taking its hand off the wall. If the agent chooses to use
its right hand then it will always be taking right hallways. If
the agent chooses the left hand, then it's always going to be taking
left hallways.

This is my implementation for the wall follower algorithm.

def wall_follower_walk(agent: Agent, maze: Maze) -> None:
  # 1. Get the current room the agent is in.
  current_room = maze.cell(agent.location)

  # If the agent is at the entrance or exit of the maze, then stop.
  if current_room is maze.starting_cell or current_room is maze.exit_cell:
    return;

  # 2. Find the agent's current orientation.
  current_orientation: dict[Orientation, Direction] = DIR_ORIENTATION[agent.facing]

  # 3. Find all the walls that have doors in that room.
  possible_directions: List[Direction] = current_room.open_sides()

  # 4. Use the wall follower strategy to pick the next room.
  if current_orientation[Orientation.RIGHT] in possible_directions: # Is there a door to the right?
    next_direction = current_orientation[Orientation.RIGHT]
  elif agent.facing in possible_directions:
    next_direction = agent.facing
  elif current_orientation[Orientation.LEFT]  in possible_directions: # Is there a door to the left?
    next_direction = current_orientation[Orientation.LEFT]
  elif current_orientation[Orientation.BEHIND] in possible_directions: # Go back the way we came?
    next_direction = current_orientation[Orientation.BEHIND]
  else:
    raise Exception("We\'re walled in! No possible doors found.")

  # 4. Find the location of the room the open door connects to.
  next_location: Point = maze.find_adjacent_neighbor(next_direction, agent.location)

  # 5. Move the agent to the next room.
  agent.face(next_direction)
  agent.move_to(next_location)

As you can see in the GIF below, the wall follower easily out performs the clueless walker. However, the wall follower can take a long time to exit the maze. I’ve put the arbitrary constraint of limiting the agents to 200 steps. Sometimes the wall follower can not escape the 400 room maze in that limit.

A* Path Finding#

The last technique that I want to try for improving the maze traversal is path finding. The A* algorithm is a popular choice for my type of use case. However, implementing A* is more complicated to implement from scratch. While researching how to implement the algorithm I found the following books to be helpful.

• Artificial Intelligence: A Modern Approach
  by Stuart Russell and Peter Norvig
• Algorithms in a Nutshell
  by George T. Heineman, Gary Pollice, and Stanley Selkow
• Game Programming Gems I: The Basics of A* for Path Finding
  by Bryan Stout

A* Implementation Considerations#

The books listed above go into more detail about the A* algorithm than I care to rehash here. My understanding of the general algorithm is:

Assume you know the location of where you're starting and the target goal (i.e. the maze exit).
Given the maze represented as a connected graph of rooms (i.e. path steps), find the optimal path
from the starting location to the target.

Track
- The Open List: Potential steps in the path.
- The Closed List: Rejected steps in the maze.

Define Functions
- cost(A, B): Define a heuristic function that calculates the cost of
              using that step in the path.

Initialize:
  start: Point # The initial point
  open: List
  closed: List

  start.cost_from_start = 0
  start.cost_to_target = cost(start, target)
  start.total_cost = start.cost_from_start  + start.cost_to_target

  open.add(start)

while open is not empty:
  current_step = Step from the top of the Open List
  if current_step is the target:
    We've found the path!
    return Success and build_path(current_step)

  Remove the current_step from the Open list.
  Add the current_step to the Closed list.

  for each possible_step in connected_rooms(current_step):
    if possible_step is in Closed List:
      Ignore this Step

    possible_step_cost = current_step.total_cost + cost(current_step, possible_step)

    if possible_step is already in the open list and the possible_step_cost is < cost(start, possible_step):
      Remove from open list as the new path is better.

    if possible_step is in the closed list and the possible_step_cost is < cost(start, possible_step):
      Remove from closed list as the new path is better.

    if possible_step is not in the open list and not in the closed list:
      possible_step.total_cost =  possible_step_cost + cost(possible_step, target)
      add possible_step to the open list

return Failure, could not find a solution.

As you can see in the pseudo code, A* has a lot going on. There are different ways it could be implemented. Here are the key features of my implementation.

Heuristic Functions#

The A* algorithm leverages a heuristic function to evaluate the cost of potential steps in the optimal path. Since my use case is finding a path in a 2D grid I’m using the Manhattan distance as the basis of my heuristic. This is my implementation of calculating Manhattan distance between to locations in a maze.

def find_distance(a: Point, b: Point) -> float:
  """Calculates the Manhattan distance between two locations."""
  return abs(a.x - b.x) + abs(a.y - b.y)

Since the maze is in two dimensions, a path can be thought of as a series of moves on a grid like a chessboard. Each step on the board has a cost of all the previous steps plus the Manhattan distance from the new step to the target.

cost_to_add_step_to_path = last_step.total_cost() + find_distance(last_step.point, potential_step.point)
potential_step.cost_from_start = cost_to_add_step_to_path
potential_step.cost_to_target = find_distance(potential_step.point, target)

The total cost a step has is then the sum of the step’s cost_from_start and cost_to_target.

A* is pretty cool because the heuristic function is not explicitly defined. This gives a lot of flexibility to the developer to craft an implementation that fits their use case. Checkout Marco Pinter’s excellent essay Towards More Realistic Pathfinding for pointers on how to craft realistic paths using A*.

Key Data Structures#

The A* pseudo code above leverages an open list and closed list. For my little maze traversing agent, I leverage a priority queue for the open list and a Python Set for the closed list.

A priority queue is useful for the open list because it enables storing the list of possible path steps as a sorted list in which the steps are sorted by their total cost.

Python doesn’t have a priority queue in its standard library, but it’s straightforward to build one using the heap functions in the heapq module.

class PriorityQueue:
  """A priority queue implemented with a min heap."""
  def __init__(self):
    self._items: List[PriorityPoint] = [] # A min heap.
    self._index: Dict[Point, PriorityPoint] = {} # An index of the points in the heap.
    self._counter = itertools.count() # A counter for tracking the sequence of points.

  def __str__(self) -> str:
    return self._items.__str__()

  def push(self, point: Waypoint, cost: float) -> PriorityQueue:
    """
    Add a point to the priority queue. Points are arranged in the queue
    by their associated cost. The item with the smallest cost is listed first.
    If a point is already in the queue, it is removed first before adding it.

    Returns
    The instance of the priority queue.
    """

    if point in self._items:
      self.remove(point)

    count = next(self._counter)
    entry = [cost, count, point]
    self._index[point] = entry
    heappush(self._items, entry)
    return self

  def pop(self) -> Tuple[float, Waypoint]:
    """
    Removes the point in the queue with the smallest cost.

    Returns
    A tuple of the cost and point.

    Throws
    Raises a KeyError if called on an empty queue.
    """

    # There could be removed points, so keep popping until a point is found.
    while len(self._items) > 0:
      cost,_ignore,point = heappop(self._items)
      if point is not REMOVED_POINT:
        return (cost, point)
    # If the queue is exhausted, then throw an exception.
    raise KeyError('Cannot pop from an empty priority queue.')

  def __contains__(self, point: Waypoint) -> bool:
    """
    Determines if a point is already in the queue.

    Example
    p in queue
    """
    return point in self._index

  def __len__(self) -> int:
    """
    Supports using the len() with the priority queue.

    Returns
    The length of the queue.
    """
    return len(self._items)

  def remove(self, point: Waypoint) -> PriorityQueue:
    """
    Removes a point from the queue if it exists. Does nothing if the point
    doesn't exist in the queue.

    Returns
    The instance of the priority queue.
    """
    if point in self._index:
      entry = self._index.pop(point)
      entry[2] = REMOVED_POINT

Decorator Pattern#

One thing that wasn’t clear to me when I was initially studying the A* algorithm is how the actual path is constructed from the various steps evaluated in the open and closed lists.

The trick is that each step needs to have a pointer to the previous step. As steps are being evaluated, the pointer is updated to reflect the current path. Then, when the last step is found a path can be constructed by following the pointers.

However, adding a pointer to a location isn’t straightforward.

In my little maze program a location is represented by a NamedTuple.

class Point(NamedTuple):
  x: int
  y: int

Because I’m using multiple path finding algorithms in the program I don’t want to expand this definition to include things just for A*. To avoid cluttering up the Point class I use the decorator pattern to wrap Point.

class Waypoint:
  """A decorator class that wraps a Point to enable chaining points."""
  def __init__(self, point: Point, predecessor: Waypoint = None):
    self._point = point
    self._predecessor = predecessor
    self._cost_from_start = 0
    self._cost_to_target = 0

  @property
  def point(self) -> Point:
    return self._point

  @property
  def predecessor(self) -> Point:
    return self._predecessor

  @predecessor.setter
  def predecessor(self, predecessor: Point) -> None:
    self._predecessor = predecessor

  @property
  def cost_from_start(self) -> None:
    return self._cost_from_start

  @cost_from_start.setter
  def cost_from_start(self, cost: float) -> None:
    self._cost_from_start = cost

  @property
  def cost_to_target(self) -> None:
    return self._cost_to_target

  @cost_to_target.setter
  def cost_to_target(self, cost: float) -> None:
    self._cost_to_target = cost

  def total_cost(self) -> float:
    return self.cost_from_start + self.cost_to_target

  def __str__(self):
    pred_str = f'({self._predecessor.x}, {self._predecessor.y})' if self._predecessor else 'None'
    return f'Waypoint (x = {self.point.x}, y = {self.point.y}) with predecessor {pred_str}'

  def __repr__(self) -> str:
    return self.__str__()

  def __eq__(self, other: object) -> bool:
    """For equality checks, only consider the decorated point, not the predecessor."""
    if (isinstance(other, Waypoint)):
      return self.point.x == other.point.x and self.point.y == other.point.y
    return False

  def __hash__(self) -> int:
    return self.point.__hash__()

This works OK for the maze experiment. However, it’s a leaky encapsulation. I directly expose the wrapped point to pass to various functions. If I was doing this for a long term project I’d work harder to define cleaner abstract data types.

Closures#

Using a path finding algorithm like A* is fundamentally different from the
first two approaches. The Clueless Walker and the Wall Follower both take one action per animation frame.

A path finding solution is different in the aspect that the entire path is determined in a single frame. The agent then simply traverses the path, one step per frame.

To keep things simple, I cheat a bit and have the agent calculate the path before the animation starts. In an active game, the path would be calculated during a single game frame or spread out over a few frames.

Just like the decorator pattern used to wrap the Point tuple, I don’t want to expand the definition of Agent to have knowledge about paths or specific algorithms.

To keep the responsibilities separate, I use a closure to bundle a generated path with a function that the agent can use to navigate the path, one step per frame.

def build_path_walker(path_to_walk: Path):
  """A closure that enables an agent to traverse a list of points."""
  path = path_to_walk
  current_step_index = -1

  def walk_path(agent: Agent, maze: Maze) -> None:
    """The Agent's maze strategy function."""
    nonlocal current_step_index, path

    if current_step_index < (len(path) - 1):
      current_step_index += 1
      agent.move_to(path[current_step_index])

  return walk_path

Building a Path Finder Agent#

Here is how the path finder agent is constructed.

path_finder = Agent('yellow')
path_finder.move_to(common_starting_point)
path_finder.face(Direction.SOUTH)

found_path, escape_path = find_path_with_a_star(path_finder, maze, maze.exit_cell.location)
if not found_path:
  raise Exception('Failed to find a path.')

path_walker = build_path_walker(escape_path)
path_finder.maze_strategy(path_walker)

Putting it all Together#

Finally, all the supporting components have been built. It is now a simple matter of putting them all together to have 3 different approaches to escaping the maze in a game loop.

# Note: 1000/125 = 8 Frames Per Second
SLEEP_TIME_SEC:float = 0.125
NUM_FRAMES = 200

# 1. Generate a maze.
maze: Maze = Maze(20, 20)
generate_maze_walls(maze)

# 2. Create 4 layers of canvases. 0: Maze, 1: A* Path, 2: Agents, 3: HUD
mc = MultiCanvas(n_canvases=4, width=800, height=400)
display(mc)

# 3. Create NPCs with different strategies
common_starting_point = Point(int(maze.width/2), int(maze.height/2))

wall_follower = Agent('blue')
wall_follower.maze_strategy(wall_follower_walk)
wall_follower.move_to(common_starting_point)
wall_follower.face(Direction.SOUTH)

random_walker = Agent('green')
random_walker.maze_strategy(clueless_walk)
random_walker.move_to(common_starting_point)
random_walker.face(Direction.SOUTH)

# Calculate a path using A*
path_finder = Agent('yellow')
path_finder.move_to(common_starting_point)
path_finder.face(Direction.SOUTH)

found_path, escape_path = find_path_with_a_star(path_finder, maze, maze.exit_cell.location)
if not found_path:
  raise Exception('Failed to find a path.')

path_walker = build_path_walker(escape_path)
path_finder.maze_strategy(path_walker)

agents = [wall_follower, random_walker, path_finder]

# 4. Do an Initial Render
draw_maze(maze, mc[0])
draw_path(escape_path, mc[1], 'red')
draw_agents(agents, mc[2])

# 5. The Animation Loop
for frame in range(NUM_FRAMES):
  for agent in agents:
    agent.explore(maze)
  draw_agents(agents, mc[2])
  draw_legend(mc[3],frame)
  time.sleep(SLEEP_TIME_SEC)

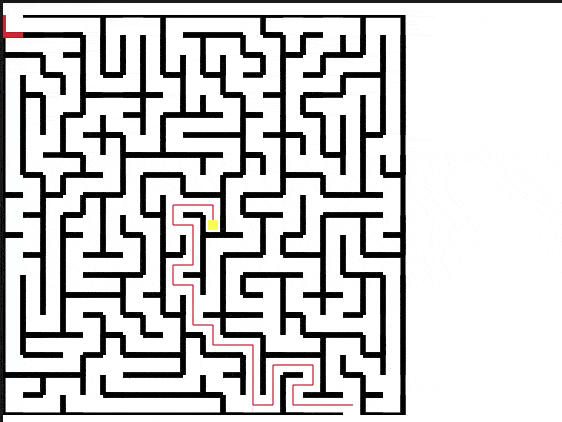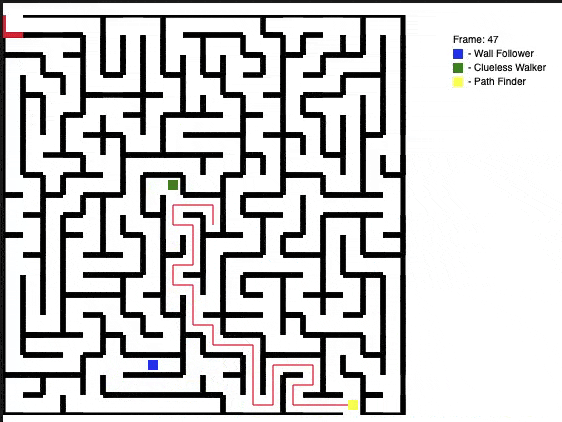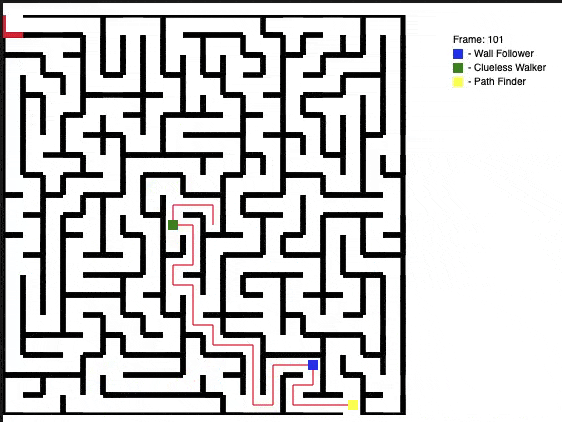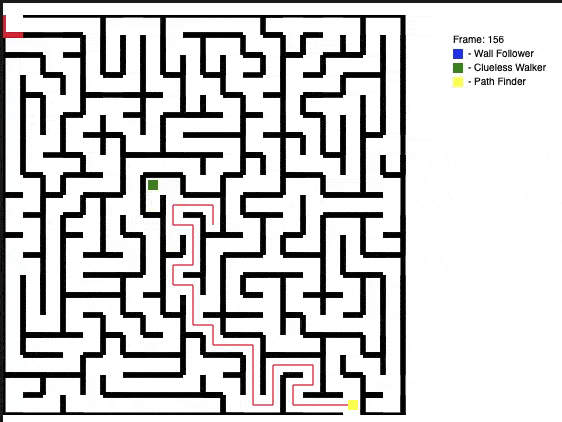
A different maze is generated each time the program runs. This time, there happened to be a short path to the exit. The path finder agent using the A* approach is the clear winner and makes a quick escape. The wall follower eventually finds it’s way to the exit, but the clueless walker lives up to its name and dies tragically in the maze.

Going Forward#

I’m happy with this definition of agents. It gets the job done and sets things up for creating more sophisticated agents for other tasks in the future. I’m keen to explore adding character traits, the concept of memories, and complex planning.

I envision agents being able to do work. To that end, I’m thinking about how I might expand this definition of agents with an internal finite state machine hierarchy, Markov chains, or hierarchical task networks.

Given the composable nature of the agents, I’m thinking they’re a a good fit for creating NPCs via builder classes or functions.

Until next time…

• Sam